Full Canonical Information from Grand Potential Density Functional Theory
D. de las Heras, and M. Schmidt
Phys. Rev. Lett., 113, 238304, (2014) DOI: 10.1103/PhysRevLett.113.238304
Full text: journal, pdf
Abstract:
We present a general and formally exact method to obtain the canonical one-body density distribution and the canonical free energy from direct decomposition of classical density functional results in the grand ensemble. We test the method for confined one-dimensional hard core particles for which the exact grand potential density functional is explicitly known. The results agree to within high accuracy with those from exact methods and our Monte Carlo many-body simulations. The method is relevant for treating finite systems and for dynamical density functional theory.
Additional material/comments:
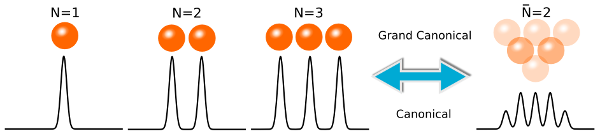
Classical density functional theory is an indispensable theoretical tool in soft condensed matter physics. It has been successfully applied to a vast
variety of systems ranging from the hard sphere fluid to e.g. pathcy colloids. The standard framework of density functional theory is the
grand canonical ensemble, where the chemical potential is fixed and the number of particles fluctuates. On the other hand, experiments and simulations are usually performed in the canonical ensemble, conserving therefore the number of particles. In the thermodynamic limit both canonical and grand canonical ensembles are equivalent. However, important differences between both ensembles arise if the number of particles of the system under consideration is small.
In this work we present a general and formally exact method to obtain the canonical partition functions and the canonical density distributions for a given grand canonical density functional. Our method can also be used to test the accuracy of density functional theories and to accelerate the minimization of grand canonical density functionals for finite systems.
Download the full text for this article: journal, pdf
Related publications:
1 Particle Conservation in Dynamical Density Functional Theory (+ info)
2 Superadiabatic forces in Brownian many-body dynamics (+ info)
