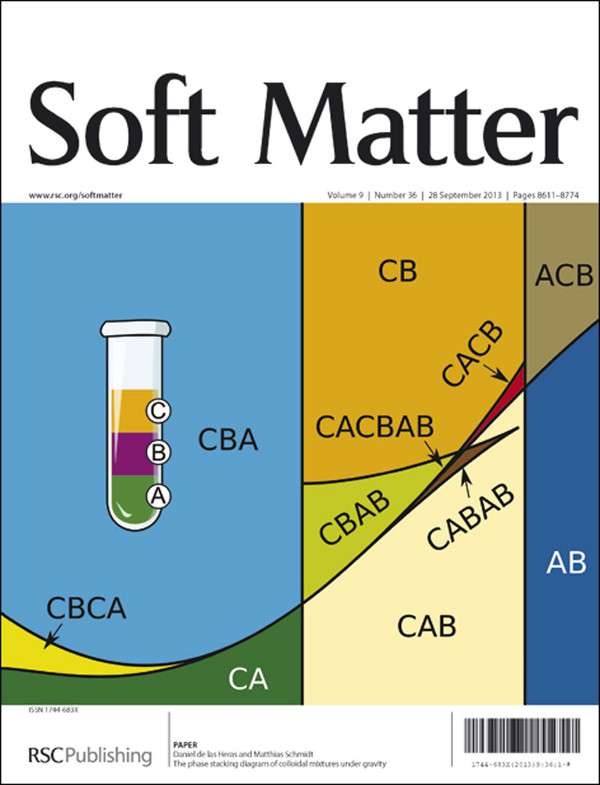
The phase stacking diagram of colloidal mixtures under gravity
D. de las Heras, and M. Schmidt
Soft Matter, 9, 8636, (2013) DOI: 10.1039/C3SM51491A
Full text: journal, pdf
Abstract:
The observation of stacks of distinct layers in a colloidal or liquid mixture in the sedimentation–diffusion equilibrium is a striking consequence of bulk phase separation. Drawing quantitative conclusions about the phase diagram is, however, very delicate. Here we introduce the Legendre transform of the chemical potential representation of the bulk phase diagram to obtain a unique stacking diagram of all possible stacks under gravity. Simple bulk phase diagrams generically lead to complex stacking diagrams. We apply the theory to a binary hard core platelet mixture with only two-phase bulk coexistence, and find that the stacking diagram contains six types of stacks with up to four distinct layers. These results can be tested experimentally in colloidal platelet mixtures. In general, an extended Gibbs phase rule determines the maximum number of sedimented layers as a function of the number of binodals and their inflection points.
Additional material/comments:
Colloidal mixtures are excellent model systems to investigate a wide variety of phenomena in Condensed Matter. Knowledge of the phase behaviour of a given mixture is often a prerequisite to understand its interfacial and dynamic behaviour. A primary means for accessing the phase behaviour is to monitor samples that have been left to settle under gravity for long enough times, such that an equilibrium between thermal Brownian motion and the buoyancy force is achieved. A standard experimental tool is to visually observe the stacking of distinct phases, and collect the observation in table or graphical form. However, there is much confusion about how to correctly draw conclusions about the bulk phase behaviour from such collected data.
In this paper we show for the first time how one can define a parameter space that characterizes the sedimentation conditions. All possible (and only those) stacking sequences are obtained from well-defined mathematical operations on the bulk phase diagram in the plane of chemical potentials.
Our results are striking in that they demonstrate that extremely rich stacking diagrams can follow from simplistic bulk phase diagrams. This implies that great care needs to be taken when drawing conclusions about the bulk phase diagram, based on observations of phase stacking sequences. In addition we show how to control the stacking sequences by varying the buoyant masses of the sample (by e.g. changing the solvent of the mixture). We have also extended the Gibbs phase rule to account for the maximum numbers of stacks under gravity.
We apply our general theory to a specific hard core platelet mixture, based on fundamental measure density functional theory. The predicted stacking diagram can be experimentally tested in binary platelet mixtures.
Download the full text for this article: journal, pdf
Related publications:
1 Sedimentation stacking diagram of binary colloidal mixtures and bulk phases in the plane of chemical potentials (+ info)
2 The role of sample height in the stacking diagram of colloidal mixtures under gravity (+ info)
3 Floating nematic phase in colloidal platelet-sphere mixtures (+ info)
4 Reentrant Network Formation in Patchy Colloidal Mixtures under Gravity (+ info)
5 Sedimentation of colloidal plate-sphere mixtures and inference of particle characteristics from stacking sequences (+ info)
6 Gravity-induced phase phenomena in plate-rod colloidal mixtures (+ info)
7 Sedimentation path theory for mass-polydisperse colloidal systems (+ info)
8 Effect of sample height and particle elongation in the sedimentation of colloidal rods (+ info)