Mesophase formation in a system of top-shaped hard molecules: Density functional theory and Monte Carlo simulation
D. de las Heras, S. Varga, F.J. Vesely
J. Chem. Phys., 134, 214902, (2011) DOI: 10.1063/1.3596749
Full text: journal, pdf
Abstract:
We present the phase diagram of a system of mesogenic top-shaped molecules based on the Parsons-Lee density functional theory and Monte Carlo simulation. The molecules are modeled as a hard spherocylinder with a hard sphere embedded in its center. The stability of five different phases is studied, namely, isotropic, nematic, smectic A, smectic C, and columnar phases. The positionally ordered phases are investigated only for the case of parallel alignment. It is found that the central spherical unit destabilizes the nematic with respect to the isotropic phase, while increasing the length of the cylinder has the opposite effect. Also, the central hard sphere has a strong destabilizing effect on the smectic A phase, due the inefficient packing of the molecules into layers. For large hard sphere units the smectic A phase is completely replaced by a smectic C structure. The columnar phase is first stabilized with increasing diameter of the central unit, but for very large hard sphere units it becomes less stable again. The density functional results are in good agreement with the simulations.
Additional material/comments:
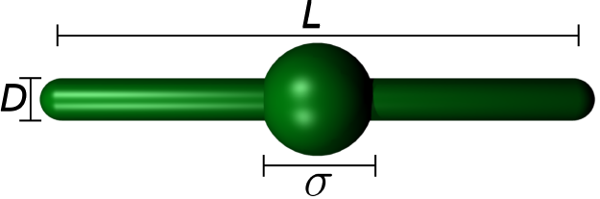
Figure: Particle geometry: A hard spherocylinder of cylinder length L and diameter D with an embedded hard sphere placed in the center of the spherocylinder.
A related poster was presented at the 8th Liquid Matter conference in Wien, Astria (2011)

Download the poster (pdf): Mesophase formation in a system of top-shaped hard molecules
Download the full text for this article: journal, pdf
Related publications:
1 Effects of wetting and anchoring on capillary phenomena in a confined liquid crystal (+ info)
2 Capillary Smectization and Layering in a Confined Liquid Crystal (+ info)
3 Capillary and anchoring effects in thin hybrid nematic films and connection with bulk behavior (+ info)
